← Back to Topics


Well model
Production-Surveillance-Intervention — Well and Network Modeling
The Beggs & Brill correlation is widely used in PROSPER to estimate pressure drop in multiphase flow. The total pressure gradient is:
\[
\frac{dP}{dL} = \left( \frac{dP}{dL} \right)_{\text{elevation}} + \left( \frac{dP}{dL} \right)_{\text{friction}} + \left( \frac{dP}{dL} \right)_{\text{acceleration}}
\]
Where:
- \(\left( \frac{dP}{dL} \right)_{\text{elevation}} = \rho_m \cdot g \cdot \sin(\theta)\)
- \(\left( \frac{dP}{dL} \right)_{\text{friction}} = \frac{f \cdot \rho_m \cdot v_m^2}{2D}\)
- \(\left( \frac{dP}{dL} \right)_{\text{acceleration}} = \frac{d(\rho_m v_m)}{dt}\)
**Image example below shows a typical VLP curve from PROSPER:**
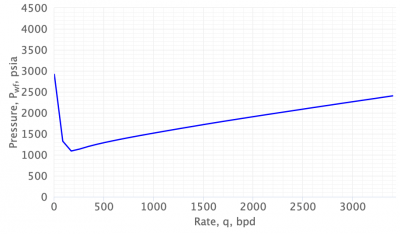
The Beggs & Brill correlation is widely used in PROSPER to estimate pressure drop in multiphase flow. The total pressure gradient is:
\[
\frac{dP}{dL} = \left( \frac{dP}{dL} \right)_{\text{elevation}} + \left( \frac{dP}{dL} \right)_{\text{friction}} + \left( \frac{dP}{dL} \right)_{\text{acceleration}}
\]
Where:
- \(\left( \frac{dP}{dL} \right)_{\text{elevation}} = \rho_m \cdot g \cdot \sin(\theta)\)
- \(\left( \frac{dP}{dL} \right)_{\text{friction}} = \frac{f \cdot \rho_m \cdot v_m^2}{2D}\)
- \(\left( \frac{dP}{dL} \right)_{\text{acceleration}} = \frac{d(\rho_m v_m)}{dt}\)
**Image example below shows a typical VLP curve from PROSPER:**

Read More
\[
\frac{dP}{dL} = \left( \frac{dP}{dL} \right)_{\text{elevation}} + \left( \frac{dP}{dL} \right)_{\text{friction}} + \left( \frac{dP}{dL} \right)_{\text{acceleration}}
\]
Where:
- \(\left( \frac{dP}{dL} \right)_{\text{elevation}} = \rho_m \cdot g \cdot \sin(\theta)\)
- \(\left( \frac{dP}{dL} \right)_{\text{friction}} = \frac{f \cdot \rho_m \cdot v_m^2}{2D}\)
- \(\left( \frac{dP}{dL} \right)_{\text{acceleration}} = \frac{d(\rho_m v_m)}{dt}\)
**Image example below shows a typical VLP curve from PROSPER:**

The Beggs & Brill correlation is widely used in PROSPER to estimate pressure drop in multiphase flow. The total pressure gradient is:
\[
\frac{dP}{dL} = \left( \frac{dP}{dL} \right)_{\text{elevation}} + \left( \frac{dP}{dL} \right)_{\text{friction}} + \left( \frac{dP}{dL} \right)_{\text{acceleration}}
\]
Where:
- \(\left( \frac{dP}{dL} \right)_{\text{elevation}} = \rho_m \cdot g \cdot \sin(\theta)\)
- \(\left( \frac{dP}{dL} \right)_{\text{friction}} = \frac{f \cdot \rho_m \cdot v_m^2}{2D}\)
- \(\left( \frac{dP}{dL} \right)_{\text{acceleration}} = \frac{d(\rho_m v_m)}{dt}\)
**Image example below shows a typical VLP curve from PROSPER:**

Read More
💬 Comments
✍️ Leave a Comment